What are bar models? Where did they come from?
Bar models have been part of the Singapore Ministry of Education’s mathematics’ concrete, pictorial, abstract process since the late 1980s.
Their origins date back further than the late 1980s, though. They were used as part of the American psychologist and educationalist, Jerome Bruner’s three-part lesson process in the late-1960s. (To learn more about three-part lessons, please read our blog that delves deeper into the concrete, pictorial, abstract approach to mathematics teaching and learning.)

Bar models have more recently become popularised in the UK and North America due to the push for better PISA rankings for mathematics by the governments of the UK, US and Canada, specifically by applying Singaporean teaching and learning strategies in their schools.
Different ways of using bar models
Bar models can be used by children (and grown-ups, too!) for a variety of uses: partitioning numbers in place value, all four operations individually (addition, subtraction, multiplication and division), multi-step and mixed operation questions, fractions, percentage increases and decreases, times tables, calculating missing angles and much, much more!
When it comes to progressing from using physical equipment (concrete), to pictorial (sketched) learning into abstract mathematics, bar models are one of the key structures that work as a bridge throughout the process. They can be used with concrete equipment, in a purely pictorial way, and as an aide-memoire when writing abstract number sentences.
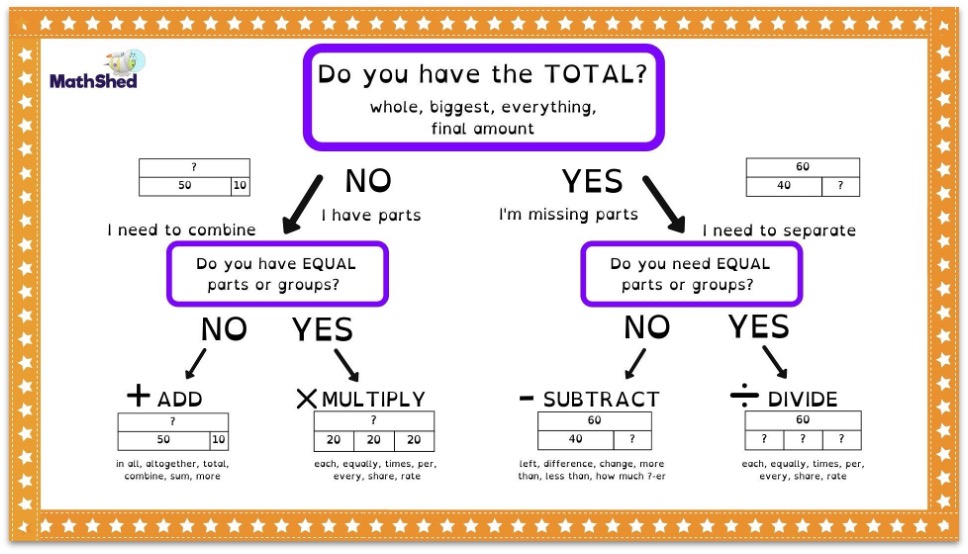
Using the bar model flow chart to unpack RUCSAC
RUCSAC is an acronym that has been popular for teachers to help children unpick word problems.
Read the question carefully
Underline keywords in the question
Choose the required operation(s)
Solve the problem
Answer the problem
Check your answer
Many teachers have fallen out of love with RUCSAC, particularly because underlining the keywords is quite a vague instruction. (Or, on some posters, even worse, understanding the question.)
The following flow chart helps to unpack and repurpose RUCSAC to the point of usefulness once more.
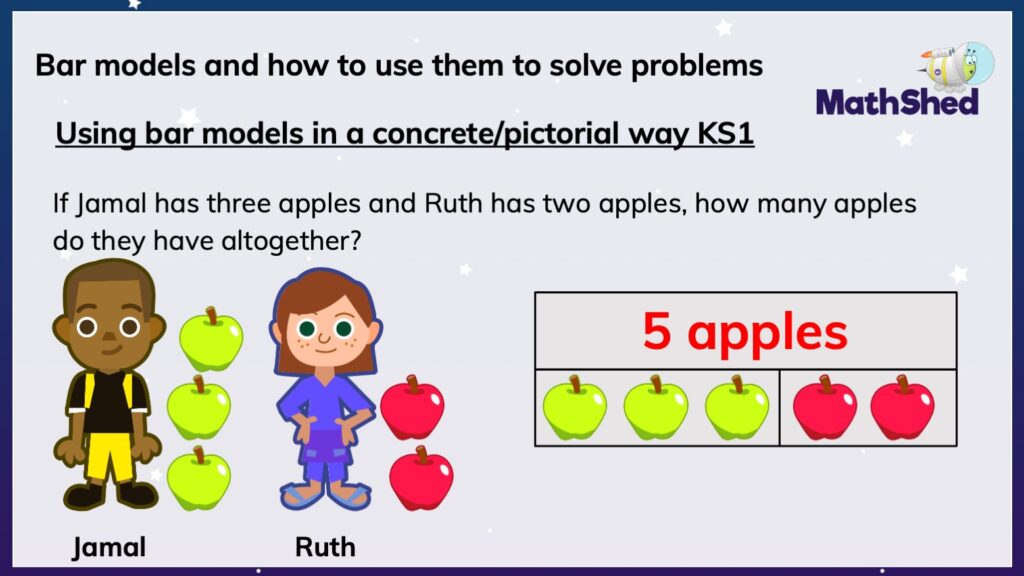
Using bar models in a concrete/pictorial way in KS1
Take the following word problem:
If Jamal has three apples and Ruth has two apples, how many apples do they have altogether?
To help children solve this problem, we could use a bar model and mathematical equipment. You could use either real apples, counters, cubes, or similar, as represented in the solution below. Shown in the Number Stacks video later in the blog is another handy resource: prepared bar model frames.
Using bar models in the “standard” pictorial way in KS1
We are presented with the same word problem, but this time, the bar model itself carries the pictorial nature of the solution.

Both parts hold numbers and the total bar holds also a number by itself, without the familiar unit of measurement (apples).
Using bar models in a pictorial/abstract way in KS1
Finally, with the same word problem in mind, we can see how using the bar model supports children in progressing to using abstract number sentences, with the + and = symbols employed in this scenario.

Using bar models in a concrete/pictorial way in KS2
If a picture is worth a thousand words, this wonderful video by Number Stacks is worth at least a million words in demonstrating best practices in using bar models in a concrete/pictorial manner in KS2. In this instance, focusing on fractions of amounts.
When it comes to bar models… plain paper is better than grid/squared paper!
Ultimately, bar models should lower the cognitive load of children. Using bar models should allow them to work through problems more quickly, not slow them down.
If a child is working out how many squares in their grid/square paper exercise book they need to use to draw the bar model, then this thinking is slowing them down.
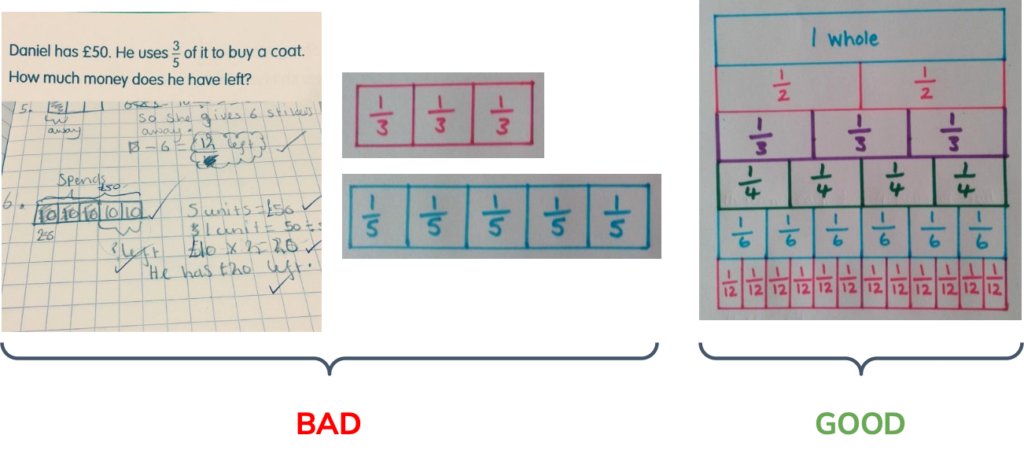
The only time you want a series of bar models to have a difference in width between their total length is if children are using comparison bars or are working on a multi-step problem and have subtracted an amount in a previous step (or enlarged the total part if adding or multiplying later on in a multi-step problem).
Regardless, using plain paper allows children to create approximate equivalence and difference between bar models while maintaining a fluent, or near-fluent, pace in their working out.
Fixed policy vs. varied bar model presentation
Some schools and schemes will advocate for one type of bar model usage over another.
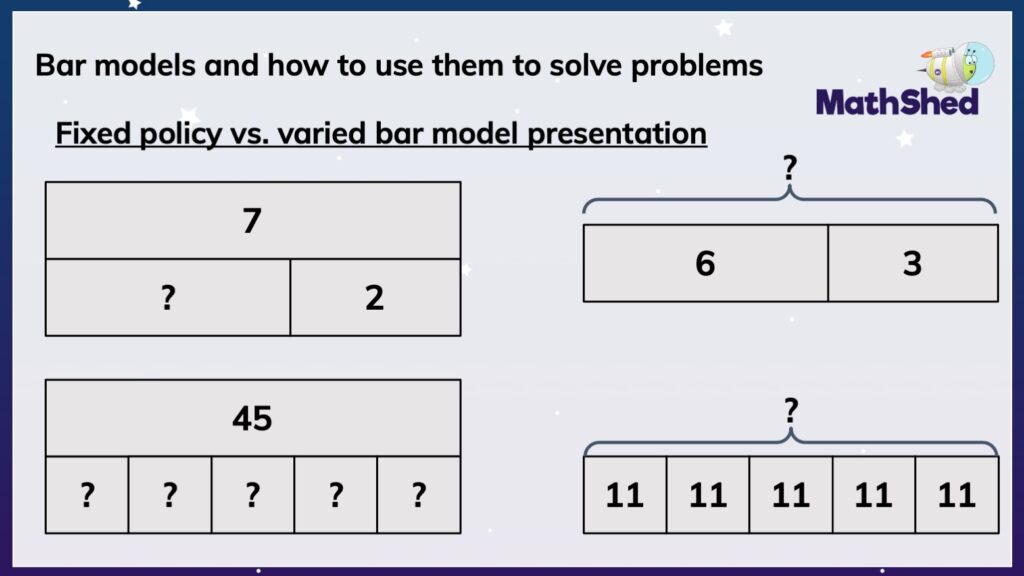
Some might exclusively use bar models like those shown on the left of the slide above, while others might favour bars curly brackets, and double arrow-headed lines, as on the right-hand side of the slide.
There is certainly strength in having a consistent and preferred set of representations for children to become confident with initially; however, ultimately, it serves children best to be aware of a range of representations, especially given the various familiar and less familiar ways bar models are presented in the end of key stage assessment papers.
Part-part-whole bars vs. comparison bar models
The use of part-part-whole bars versus bars with curly brackets is particularly apparent when performing subtraction calculations.

Here, the following word problem has been posed: “If Ahmed and Eve have 8 oranges in total and Ahmed has five oranges, how many oranges does Eve have?”
So, using our bar model flow chart, we can draw up a part-part-whole bar model.
Do you have the total? Yes. So, we put 8 in the total bar.
Do we have parts or are we missing a part? We are missing Eve’s part.
Are the parts equal or unequal? We do not know yet, but it is likely that they are unequal. So, we know to draw a bar model for subtraction, as shown above (on the left-hand side of the slide).
Similarly, we can use a comparison bar model, as we are seeking to find the difference between the total amount of eight apples and Ahmed’s five apples. (Shown on the right-hand side of the slide.)
Either way, an adult modelling or children solving the word problem using either type of bar model should arrive at the correct answer. Eve has three apples.
Using bar models for subtraction in KS2
Bar models can be used for each of the four operations in KS2 (as well as multi-step, mixed operation problems, and more).
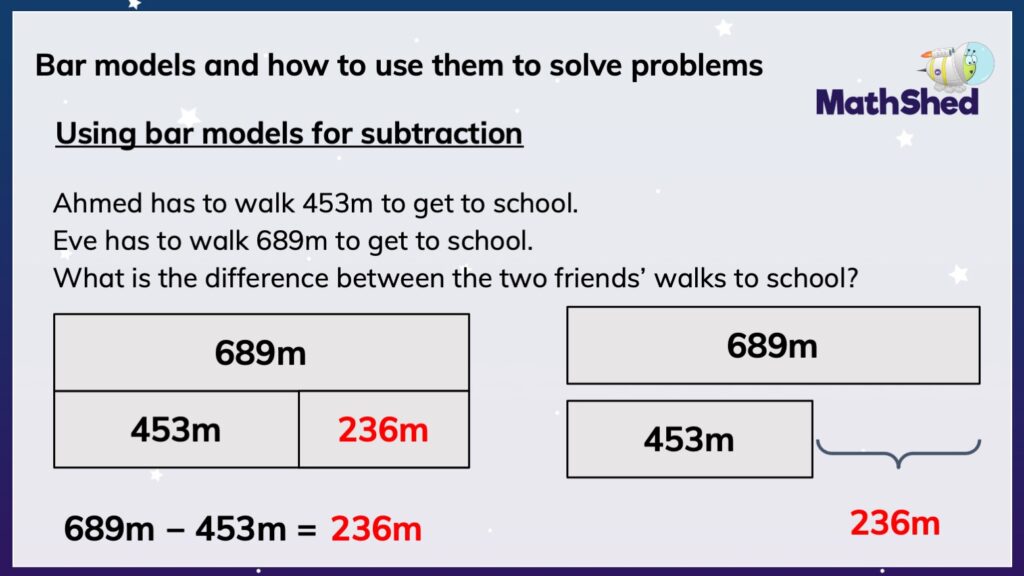
We have provided a similar subtraction word problem. Now the complexity has increased, as we are dealing with three-digit numbers and a unit of measurement, too.
Ahmed has to walk 453m to get to school.
Eve has to walk 689m to get to school.
What is the difference between the two friends’ walks to school?
Again, using our bar model flow chart, we can draw up a part-part-whole bar model.
Do you have the total? Yes. We know that Eve’s walk to school is the greatest distance. So, we will put 689m in the total bar.
Do we have parts or are we missing a part? We are missing the difference amount between the two friends’ walking distances to school. So, we will place Ahmed’s measurement of 453m in the known part bar.
Are the parts equal or unequal? Again, we do not know yet, but it is likely that they are unequal. So, we know to draw a bar model for subtraction, as shown above (on the left-hand side of the slide).
Much like the simpler subtraction word problem above, we can use a comparison bar model, as we are seeking to find the difference between Eve’s walk to school and Ahmed’s walk to school. Shown on the right-hand side of the slide is the comparison bar model.
Whether adults or children use the part-part-whole bar model or comparison bar model, assuming no transcription or calculation errors are made, the correct solution will be found: 236m.
Using bar models for addition
Bar models can be used to help solve addition calculations for all primary year groups.

Once more, we can use the bar model flow chart to help draw the bar model.
The word problem is:
James has 237 tokens.
Yasmin has 342 tokens.
In total, how many tokens do the two friends have?
Do we know the total? No.
Are the parts equal? No, so we know it will be a bar model for addition.
Children should then draw two unequal parts, with 237 going into the smaller part and 342 going into the larger part.
Once they have completed the calculation, they will know that 579 is the sum (total). So, 579 goes into the whole bar.
Using bar models for multiplication
Bar models can be used for multiplication, from the 2 times table, all the way through to multi-digit by single-digit multiplication.

The word problem is:
Farmer Sam has four cows.
On average, each cow weighs 360 kg.
How much do the cows weigh combined?
Here, we can use the bar model flow chart questions to help with demonstrating using bar models for multiplication.
Do we know the total? No.
Are the parts equal? Yes, so it is a multiplication calculation.
Next, do we know how many parts there are and how much each part is worth? Yes, four lots of 360kg.
So, using this information, children should be able to draw a bar model with four equal parts with 360kg in each part. Doing so should help them either mentally multiply or make jottings of repeated addition. The result, as shown, is 1,440kg.
Using bar models for division
Just as we have seen bar models used for addition, subtraction and multiplication, they work wonders for division, too!

The word problem is along a similar farmyard theme as the previous word problem:
Farmer Sam has six rams that are all the same weight.
In total, the six rams weigh 672 kg.
How much does one ram weigh?
Do we know the total? Yes.
Are the parts going to be equal? Yes.
(And, into how many parts do we need to split the total? Six.)
So, in this case, children should then be able to start drawing their bar model with the total bar holding 672kg. They should then know to draw six equal part bars beneath the total bar.
If they are using mental strategies or a quick bus stop division calculation, children should then be able to write 112kg in each of the six parts, as well as after the equals symbol in a number sentence.
Using bar models for fractions of amounts
Bar models being used for fractions of amounts are covered in the Number Stacks video above, too.
When working with fractions of amounts, children will either be asked to find a unit fraction amount (one-third, one-fifth etc.) or a non-unit fraction amount (three-quarters, seven-tenths etc.). If it is a unit fraction of an amount problem, it requires the same as a division bar model solution, but when it is a non-unit fraction of an amount word problem, it requires a multi-step solution.

The word problem is:
James had 355 marbles at the beginning of the year.
By the end of the year, he has two-fifths of his marbles left.
How many marbles has James lost?
We can use the bar model flow chart questions to start helping us solve the problem.
Do we know the total? Yes. So, we can start by drawing a total bar with 355 written inside it.
Are there equal parts? Yes, we know we are going to be working with fifths, so there will be five equal parts.
Initially, the total, 355, needs to be divided by 5, meaning each of the five parts is worth 71.
We then know that James has two-fifths of his marbles left, meaning he has lost three-fifths of his marbles.
So, the final step (shown above by a curly bracket, but could have been a second bar model), demonstrates three equal parts of 71.
3 × 71 = 213. Therefore, James lost 213 marbles.
Using bar models to calculate percentages
Calculating percentages with bar models is a derivative of the division bar model.

The word problem is:
At full price, a pair of shoes cost £60.
The price is reduced by 20% in the summer sale.
How much do the shoes cost in the summer sale?
Again, we can work through the bar model flow chart questions.
Do we know the total? Yes, £60. So, £60 goes into the total bar.
Is there equal or unequal parts? Using known facts, that 20% is equivalent to one fifth, children should then know to split the part bar into five equal parts.
Children can then use their times tables knowledge to divide 60 by 5, to state that 20% of the full price is £12.
Then, there is the option to either multiple £12 by 4, or subtract £12 from £60. Either way, the correct solution can be found: the shoes will cost £48 in the sale.
Using bar models for algebra
Bar models work wonderfully for algebra. They can be used for working with formulae, expressing rules, solving equations and much more!
Here, we look at using bar models to work out an unknown value.

We can answer the initial bar model flow chart question to start with…
Do we know the total? Yes. So, we can put 22 into the total bar.
Do we know any of the parts? Are any of them equal? Well, we know one of the parts is 4. We also know that there are two equal unknown parts, too.
So, we draw the topmost bar model on the right-hand side of the slide above to start.
We can then subtract the known part value, 4, from the total, 22, to get the difference, 18.
Then, we can draw a second bar model, as shown on the bottom right-hand side of the slide. Initially, as 18 in the total bar, and a ‘y’ in each of the two equal, unknown part bars.
Then, it’s a matter of dividing 18 by 2 to solve the equation and know that each ‘y’ is worth 9.
Using bar models to solve multi-step word problems
A bar model, or series of bar models, is a great structure for solving multi-step word problems.

The word problem is:
A papaya weighs 700g. A watermelon weighs twice as much.
a) What is the weight of the watermelon?
b) What is the total weight of the papaya and watermelon combined?
Here, we can see the pupil is using free-form bar models and curly brackets, rather than the part-part-whole bar models we have seen in the majority of the blog.
The pupil has drawn what is known already: a bar representing the weight of a papaya, 700g.
He has then drawn two bars each roughly as wide as the papaya bar. He knows that the weight of the watermelon is double the weight of the papaya. So, he can calculate that 700g × 2 = 1,400g to find the weight of the watermelon.
Next, all he has to do is combine the two weights together to solve the second part of the word problem. Then, he is ready to show that the total weight of a papaya and a watermelon combined is 2,100g.
Using bar models to calculate missing angles
The strength of bar models is their versatility. It isn’t just when teaching addition, subtraction, multiplication and division that they are helpful! They can be used for many areas of the curriculum, including calculating missing angles.
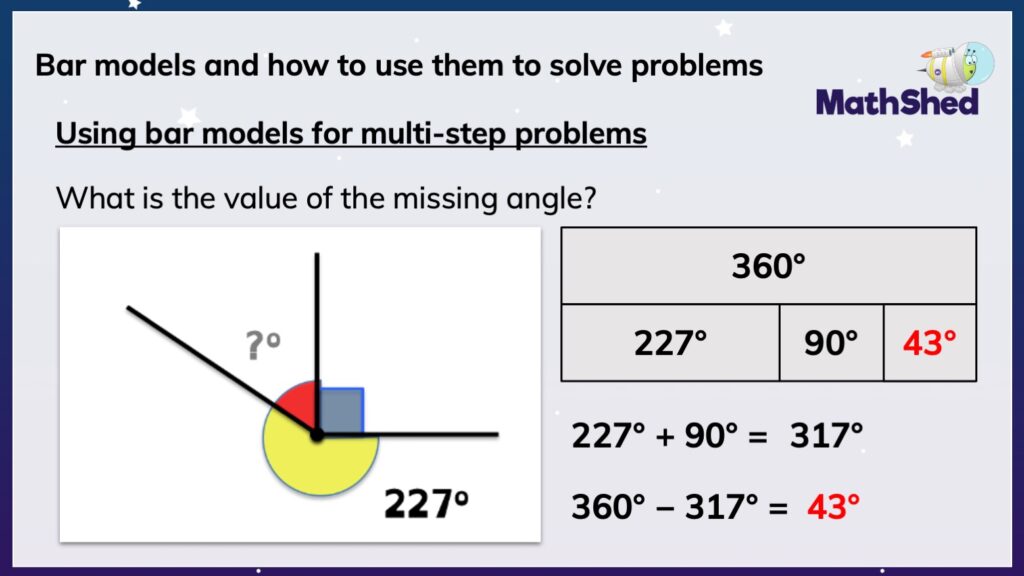
Again, we can return to the bar model flow chart questions.
Do we know the total? Yes, it should be a known fact that a full turn is equal to 360 degrees. So, we can start by writing 360 degrees into the total bar.
Do we know any of the parts’ values? Are the parts equal? Yes, we do know some of the parts. No, they are not equal.
So, then we know to draw three unequal part bars. The largest part represents 227 degrees, the next largest is the right-angle value of 90 degrees, and the smallest part should be empty to start with…
Then, it is apparent from the bar model that 227 and 90 degrees need to be combined, then subtracted from 360 degrees. So, the missing angle is 43 degrees.
Further Festive Bar Model Practice
Subscribers and non-subscribers alike can download our Advent CalenBAR resources.
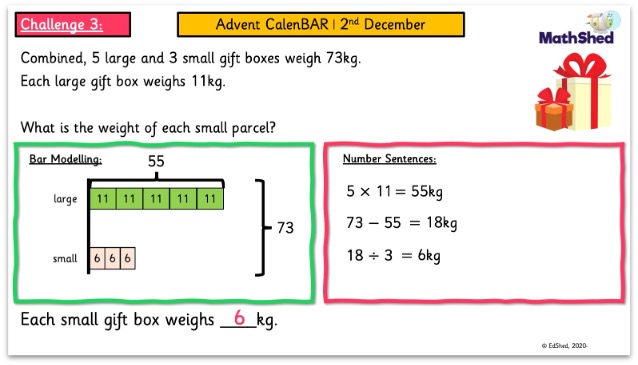
There are four daily challenges to encourage the use of bar models to solve problems. They come in PowerPoint and PDF format, with a handwriting and dyslexia-font, as well as providing question and answer pages!

